Capacitors A capacitor is an electronic device for storing charge. Capacitors can be found in almost all but the most simple electronic circuits

Capacitors

Various types of capacitor

A capacitor is an electronic device for storing charge. Capacitors can be found in almost all but the most simple electronic circuits. There are many different types of capacitor but they all work in essentially the same way. A simplified view of a capacitor is a pair of metal plates separated by a gap in which there is an insulating material known as the dielectric. This simplified capacitor is also chosen as the electronic circuit symbol for a capacitor is a pair of parallel plates as shown in Figure 1.

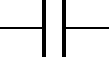
Figure 1. The symbol for an unpolarised capacitor.

Normally, electrons cannot enter a conductor unless there is a path for an equal amount of electrons to exit. However, extra electrons can be "squeezed" into a conductor without a path to exit if an electric field is allowed to develop in space relative to another conductor. The number of extra free electrons added to the conductor (or free electrons taken away) is directly proportional to the amount of field flux between the two conductors.
In this simplified capacitor the dielectric is air. When a voltage, V is applied to the terminals of the capacitor, electrons flow on to one of the plates and are taken off the other plate. The total number of electrons in the capacitor remains the same. There are just more on one the negative plate and fewer on the positive plate.

Figure 2. Charging a capacitor with a battery

If the volage were increased the increased potential difference between the plates would push more electrons on to the negatively charged plate. We could measure the charge stored on the plate as a function of different applied voltages.
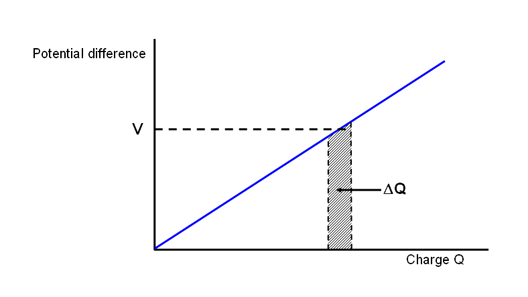
At zero voltage, the capacitor plates are neutral and so no charge is stored. (we assume that we started with a fully discharged capacitor), at a voltage V the charge on the plates is Q and at twice the voltage, the charge is doubled. We find that for increasing voltage the charge increases linearly. We can plot this as a straight line.
Suppose that we go away and do some research and come back with a better capacitor which stores more charge for a given voltage we can plot the result of the charge stored as a function of applied voltage
This would be represented as another line with a steeper slope. If we plotted lots of graphs for different capacitors we would get many straight lines. We can say that a measure of the capacitance is the how much the charge is stored for a given voltage. This is sometimes expressed as Q=CV.
Of course in charging the capacitor work must be done to move the charge. Therefore energy must be supplied and this energy is available when the capacitor is discharged.
The work done is given by W=qV. Initially the charge is easily moved onto the plates of the capacitor, however as more charge is moved onto the capacitor plates the repulsive force between the charges makes it harder to add charge, when the repulsive force of the charges equals the power of the battery, no more charge can be moved onto the plates. Therefore the average work is 1/2qV. If we look at our graph of charge against voltage we can recognise this is the same as the area under the curve. In general, the work done is equal to the energy transferred. Mathematically,

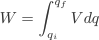
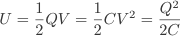
Factors Affecting Capacitance

How can we increase the capacitance of a parallel plate capacitor? There are three factors which affect the capacitance of a parallel plate capacitor.

Area

A variable capacitor

By increasing the area of the plates we can put more charge on the plates before the repulsive forces becomes a problem. Therefore, the capacitance is proportional to the overlapping surface area of the plates. In a variable capacitor the overlapping area can be increased or decreased by rotating interpenetrating plates thus increasing or decreasing the capacitance. Electrolytic capacitors have their plates etched to produce a rough surface which increases the surface area still further.

Separation

Decreasing the separation of the plates, decreases the voltage of the capacitor since the electric-field is not affected by the distance between the plates. The voltage on the capacitor is V=Ed. Therefore the voltage increases. For a constant charge, Q, C=Q/V =Q/Ed.

Dielectric Constant

The capacitance of a parallel plate capacitor is given by C=ε_r A/d, where A is the area of the plates, d is the separation between the plates and ε_r is the relative permiliability of the dielectric between the plates. The relative permiability is some factor, K multiplying the permiability of free-space ε₀. ε₀ has a value of 8.85x10^-12 F.m^-1.
A full list of relative permiabilities can be found for almost any dielectric material. The greater the relative permiability the greater the capacitance of the capacitor. Some good materials are Mica, polystyrene, oil.
ε_r=K ε₀

Capacitor Networks

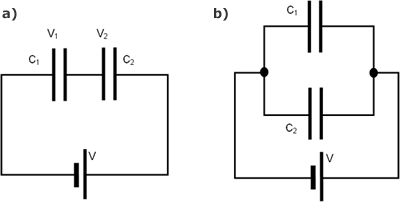
Figure 3. Capacitor networks in Series and Parallel

Series

Consider the series network of capacitors shown in Figure 3a. where the positve plate is conected to the negative plate of the next.What is the equivalent capacitance of the network? Look at the plates in the middle, these plates are physically disconected from the circuit so the total charge on them must remain constant. It follows that when a voltage is applied across both of the capacitors, the charge +Q on the positive plate of capacitor C₁ must be balanced by the charge -Q on the negative plate of capacitor C₂. The net result is that both capacitors possess the same charge Q. The potential drops V₁ and V₂ across the two capacitors are in general, different. However, the sum of these drops equals the total potential drop V applied across the input and output wires. V=V₁ + V₂. The equivalent capacitance of the pair is again C_T=Q/V. Thus, 1/C_T = V/Q = (V₁ + V₂)/Q = V₁/Q + V₂/Q giving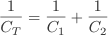

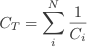
In general, for N capacitors connected in series, is

By connecting capacitors in seires you store less charge so does ever make sense to connect capacitors in series? It is sometimes done because capacitors have maximum working voltages, and with two 900 volt maximum capacitors in series, you can increase the working voltage to 1800 volts.

Parallel

For a parallel circuit such as in Figure 3b. the voltages are the same across each component. However the total charge is divided between the two capacitors since it must distribute itself such that the voltage across the two is the same. Also, since the capacitors may have different capacitances C₁ and C₂ the charges Q₁ and Q₂ must also be different. The equivalent capacitance C_T of the pair of capacitors is simply the ratio Q/V where Q=Q₁+Q₂ is the total stored charge. It follows that C_T = Q/V = (Q₁+Q₂)/V = Q₁/V + Q₂/V giving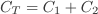

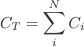
It is fairly obvious from the previous discussion that for N capacitors in parallel, the total capacitance is

The overall capacitance increases by added together capacitors in parallel so we create larger capacitances than is possible using a single capacitor. High-energy physics labs often have large banks of capacitors which can store large quantities of energy to be released in a very short time. The largest bank of capacitors in 2006, can store 50 MJ of energy.

Charging and Discharging Capacitors

A circuit consisting of a battery, a switch, a resistor and a capacitor in a series loop is called an "RC" circuit. Kirchoff's voltage law for this circuit is
V = IR + Q /C. When expressed purely in terms of the charge, this becomes
V = dQ/dt R + Q/C.
This is a differential equation, whose solution is an exponential function. When the switch is closed, the capacitor charges over time:
Q = Q_f (1 - e^-t/RC),
where Q is the charge at time t and Q_f is the final charge on the capacitor. Note that Q never equals Q_f , but as t gets extremely large, Q gets arbitrarily close to Q_f. The product RC is called the RC time constant, and is a characteristic quantity of the RC circuit. When t = RC, the capacitor has charged to a fraction (1 - 1 / e, about 63%) of its final value. It is necessary to use a time constant, and not some sort of terminal time, since the process is asymptotic. Its value is an arbitrary choice; we naturally choose a value in terms of the exponential base (when the exponent is negative one).